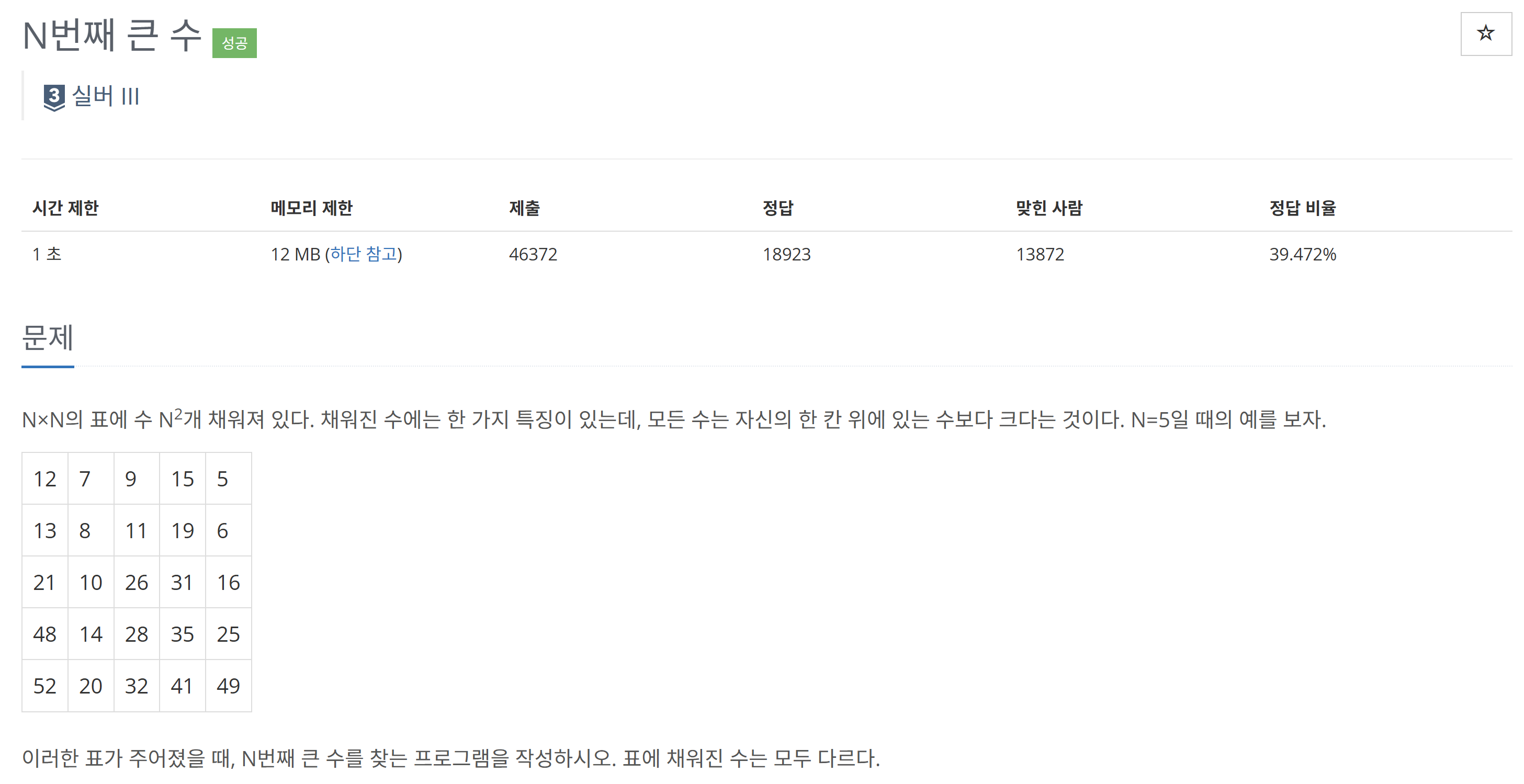
자료구조, 정렬 문제이다.
메모리 제한이 걸려 있긴 한데, 메모리를 신경쓰지 않아도 풀리긴 한다.
난 3가지 방식으로 풀어보았다.
import java.io.*;
import java.util.*;
public class N번째_큰_수_2075 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
int[] table = new int[N*N];
/** 숫자를 하나의 배열로 전부 입력받기 */
int idx = 0;
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
table[idx] = Integer.parseInt(st.nextToken());
idx++;
}
}
Arrays.sort(table); // 오름차순 정렬
/** N번째로 큰 수 출력 */
System.out.println(table[table.length - N]);
}
}
우선 첫번째 방식, 기본 배열 방식이다.
시간복잡도는 O(N^2logN) 이며, 가장 단순하고 직관적이다.
N*N 크기 하나의 배열에 모든 값을 넣고, 정렬한 후 인덱싱으로 N번째 큰 수를 찾는다. 여기서 "정렬"이 가장 큰 오버헤드를 차지한다. 정렬은 NlogN인데 N^2크기의 배열에 대해서 진행하니까.
딱히 복잡한 로직이 없고, 솔직히 이 방식은 너무 간단해서 브론즈 정도로 내려도 될 정도이다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
/** 우선순위 큐 사용 */
PriorityQueue<Integer> maxPq = new PriorityQueue<>(Collections.reverseOrder());
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
int value = Integer.parseInt(st.nextToken());
maxPq.offer(value);
}
}
/** N번째 큰 수 추출 */
int result = -1;
for (int i = 0; i < N; i++) {
result = maxPq.poll();
}
System.out.println(result);
}
}
두 번째 방식, 우선순위 큐를 활용한 방식이다.
시간복잡도는 기본 배열 방식과 마찬가지로 O(N^2logN) 이다. 일단 메모리는 조금 더 썼지만 시간은 거의 절반으로 줄어들었다.
우선순위 큐 방식의 주요 오버헤드는 최대힙 "삽입"연산에서 일어난다. 매 삽입마다 logN 인데, 이게 N^2번 진행된다.
그래서 표면적 시간복잡도는 기본 배열 방식과 같다. 그런데 왜 시간 차이가 이렇게 많이 나나 찾아보니, 기본 배열 방식에서 사용한 Arrays.sort() 메서드가 배열 크기가 커질수록 내부 구조 상 오버헤드가 더 크기 때문이라고 한다.
import java.io.*;
import java.util.*;
public class N번째_큰_수_2075_v2 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
/**
* 우선순위 큐 사용 (최소 힙)
*
* - N^2개 숫자 중 가장 큰 N개의 요소만 힙에 저장
* - 힙에 저장된 값 중 가장 작은 값이 N번째 큰 수
*/
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
int value = Integer.parseInt(st.nextToken());
// N개까지 우선적으로 저장
if (pq.size() < N) {
pq.offer(value);
}
// 큐 최소값과 value 비교해서 큰 값을 저장
else if (pq.peek() < value) {
pq.poll();
pq.offer(value);
}
}
}
/** 가장 큰 N개의 수 중, 가장 작은 값이 N번째로 큰 값이다 */
System.out.println(pq.peek());
}
}
마지막 방식, 우선순위 큐를 활용한 최소힙 최적화 방식이다.
표면적 시간복잡도는 위 2개 방식과 같다. O(N^2logN) 이다.
음 .. 근데 정확히 하면,
배열 방식: O(N^2log(N^2)
최대힙 방식: O(N^2log(N^2)
최소힙 최적화: O(N^2logN)
차이가 발생하는 부분은 최소 힙에 저장된 데이터 개수이다. 최적화 방식은 N개만 저장하고, N에 대한 logN 삽입이 일어나지만,
나머지 2개 방식은 N^2개를 저장하고 N^2에 대한 logN^2 삽입이 일어난다.
또한 최소힙 최적화 방식은, "공간복잡도" 측면에서 N^2 -> N 으로 개선된다.
그러나.. 실제 제출 시 최소힙 방식은 메모리 사용량은 개선되었으나 시간복잡도는 거의 비슷한 수준을 유지했다. 그 이유는 조건문 비교 연산 때문이다. 최대힙 방식은 조건검사 없이 무조건 offer만 하면 되지만, 최소힙 방식은 if, else if 조건 검사해서 poll, offer 여러 연산을 거치기 때문이다. 이 방식은 데이터 크기가 커질 수록 효율적인 방법이라고 생각되며, 이 문제에서는 엄청난 성능 차이를 거두진 못 했다.

맨 아래부터 배열 방식, 최대힙 방식, 최소힙 최적화 방식이다.
첫 방식인 배열과 마지막 방식인 최소힙 최적화 방식을 비교해 보면, 메모리 사용량과 시간 모두 단축된 것을 알 수 있다.
'Algorithm > Priority Queue' 카테고리의 다른 글
| [Baekjoon 11279 / python / 실버2] 최대 힙 (0) | 2024.03.26 |
|---|